電子電路知識:為什么電路中的阻抗要引入復數來表示?不理解電路、信號處理中的“虛部”怎么辦?看完秒懂
初學電子學,腦瓜里面很多疑問
為什么電容、電感的阻抗表達式要用虛數?
為什么在傅立葉變換中要有虛數?
為什么在濾波器的傳遞函數中會出現虛數?
最初遇到“虛數”的概念是在高中數學中,我大概將它看成一維(實數)到二維的擴展。書上也就是畫成兩個坐標軸來表示復數嘛。那么,為什么只有一個虛數單位i,沒有再定義一個更高級的復數來描述三維空間呢?從來沒想過。
大學學了高等代數,補充了復數域,多項式這些知識后大概知道為什么要發明出復數來補充實數的不足了。至于維數的擴展,也不是復數的用途。再后來,學了傅立葉變換之后,我對為什么要用復數來表示信號仍然沒有理解。數學上這沒有問題,數學是對世界的一種描述,是抽象出來的,又如直線、空間等等概念也是抽象出來的。但現實世界里面的物理量,電流電壓都是實際存在的,哪來的虛部呢(別扯到量子物理,不在電子工程討論范圍)?更后來修《小波分析》課的時候,有個同學在課間問了這個問題,老師說的是“采兩個信號”的意思。可是,畢竟復信號和二維信號不是一個處理方法呀。
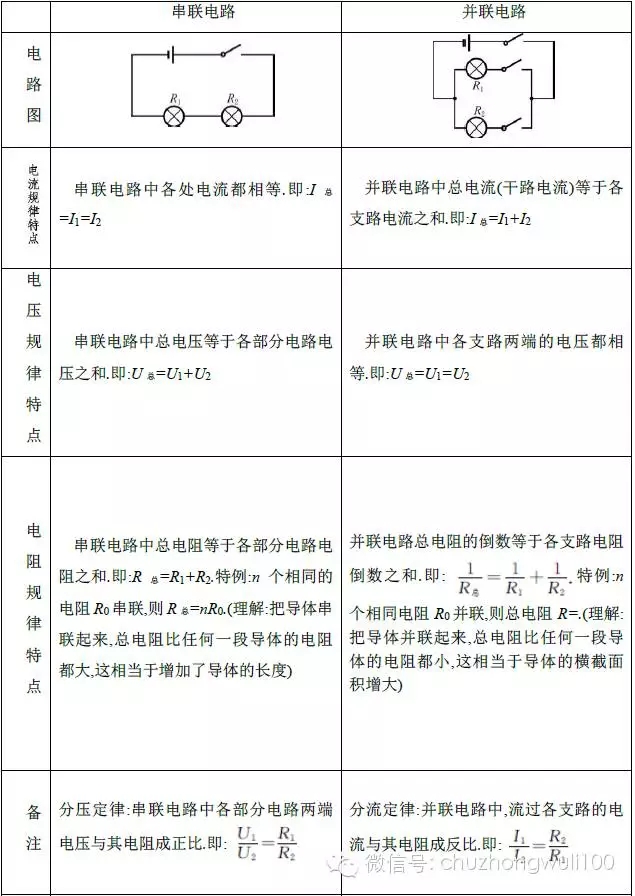
自學了些電路基礎,我才發現在電路里面用虛數是提供了很大的方便。如果不用虛數,就沒法對電容、電感使用歐姆定律了。
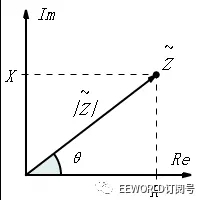
借用了虛數,將電感、電容中的電抗成分(就是和純電阻不一樣的那個交流特性)計成歐姆單位
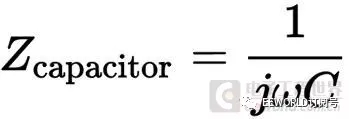
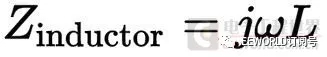
然后,歐姆定律、戴維南定理等等都可以照樣用了,甚是方便,只不過把電壓、電流也要換成復數了。
什么,電壓能有個虛部?示波器能看到這個虛部嗎?
反過來看,若不引入虛數的話,怎么處理電路中的電感和電容呢?那必然是要使用微分方程、積分方程來表達電壓和電流的關系。的確不方便啊,求解穩態電路這樣就費太多工夫了。借助拉普拉斯變換工具,看輸入和輸出關系的話,就又出來虛數了。
交流電是隨時間變化的,若用正弦函數來表達,u=Asin(ωt+θ)就包含了幅度、頻率和相位三個量。電容和電感會改變交流電的相位,因此在分析頻率特性的時候,僅用幅度描述是不夠的。虛數因為可以表示為幅值和相角的形式,剛好可以刻畫交流電輸入和輸出的關系。
說到底,這還是一個數學工具在解釋世界。正弦波就正弦波嘛,一定要虛數么?Euler公式
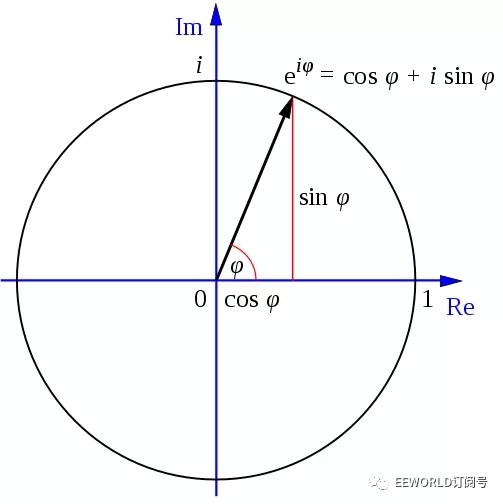
看起來很漂亮,但是對交流信號,那個憑空整出來的虛部又是什么意思?電場能是實部,磁場能是虛部?不對。
畢業數年以后,我對這個疑問的解釋是如下這樣:
世界有兩種最基本的運動形式:一種是勻速直線運動,一種是勻速圓周運動(轉動)。轉動就有了半徑、周期。如果認為勻速直線運動是一種恒定狀態,那么勻速轉動也屬于恒定的——周而復始,你只要知道了它的無限短的一段時間的運動,就能知道它的過去和未來。
也就是說,一個單一頻率的信號是可以用一個恒定轉速的圓周運動來代表的。
在平面上看這個圓周運動,它的軌跡是一個圓。
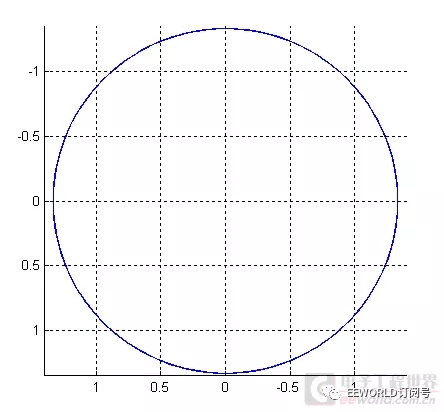
如果增加一個時間維度,想象一下,看起來是什么樣子?

一圈一圈的螺線,對了吧,沿著時間軸方向的。
再側過來一些看,更清楚一點:

再換個角度:
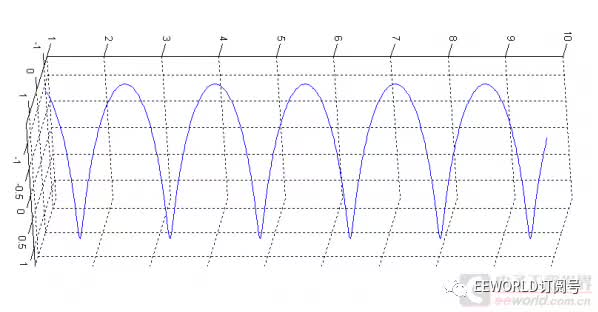
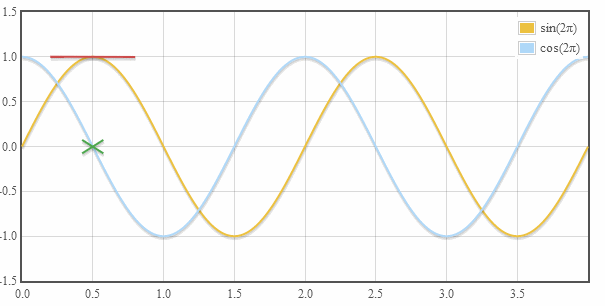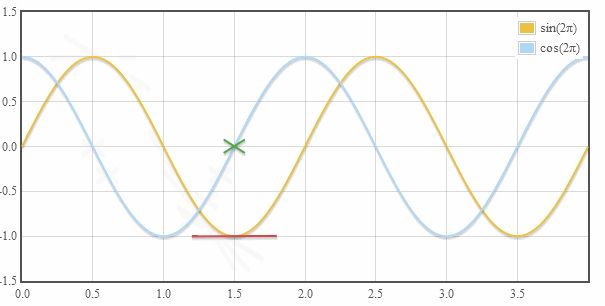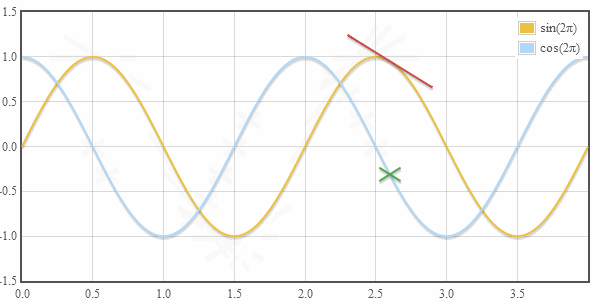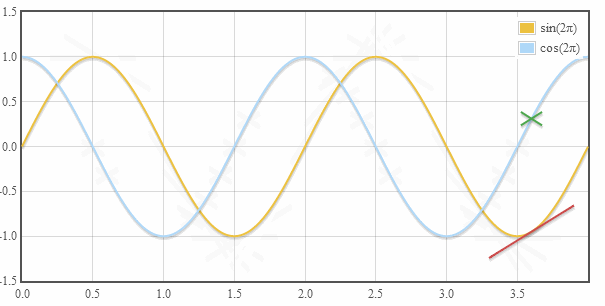
當垂直于時間軸去“看”這個圓周運動的時候,看到什么呢?
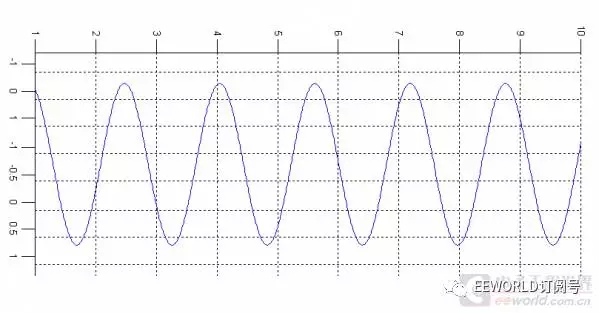
正弦型啊!換個角度也可以看到是這樣的:
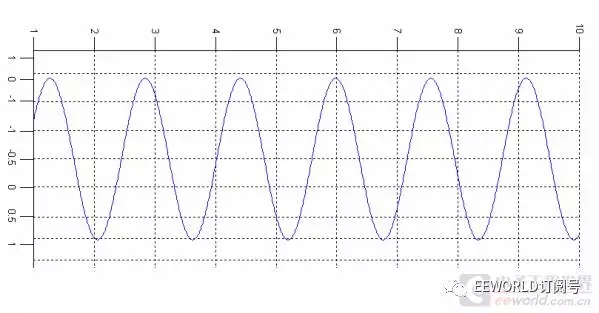
注意,正弦函數的相位發生了變化。
當我們觀察到一個正弦形的信號(電壓、電流,也可以是其它的物理量),所觀察到的認為是它的實部。假設(用腦補一下)這個信號其實是一個在轉動的信號,它還有一個對應的虛部看不見。正弦信號經過一個線性系統(黑盒子)出來之后,除了轉動半徑(幅度)可能發生改變外,轉角也會發生偏移,于是被我們觀察到的波形也產生了相位差。隨著我們觀察角度的不同,初始相位也可以不同,但是輸入和輸出的相位差是穩定的。
總結:能夠被觀察到的信號是實的,然而在補充了一個不存在的虛部之后,信號從來回振蕩的形式變成了更簡單更基本的圓周運動。復雜的信號也可以分解為很多乃至無窮多個圓周運動的疊加,我們總是從某個固定的角度去觀察的。在描述兩個同頻的圓周運動的相對關系(比如輸入和輸出)時,使用虛數可以更方便地表達幅度和相角的差異。
以上就是100唯爾(100vr.com)小編為您介紹的關于電子電路知識的知識技巧了,學習以上的電子電路知識:為什么電路中的阻抗要引入復數來表示?不理解電路、信號處理中的“虛部”怎么辦?看完秒懂知識,對于電子電路知識的幫助都是非常大的,這也是新手學習電子專業所需要注意的地方。如果使用100唯爾還有什么問題可以點擊右側人工服務,我們會有專業的人士來為您解答。
本站在轉載文章時均注明來源出處,轉載目的在于傳遞更多信息,未用于商業用途。如因本站的文章、圖片等在內容、版權或其它方面存在問題或異議,請與本站聯系(電話:0592-5551325,郵箱:help@onesoft.com.cn),本站將作妥善處理。
上一篇: 射頻電路仿真之4大方面教你設計射頻電路
下一篇: 電工高級技師報考條件是什么?
電子電路知識課程推薦
電子專業技術文檔
推薦閱讀











 向客服提問
向客服提問